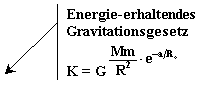Dies ist der Titel einer 85-seitigen Einführung in den neuesten Wissensstand über Gravitation. Um Ihnen ein Urteil über das Buch zu ermöglichen seien statt vieler Worte die ersten zwei Kapitel als ungekürzte Leseprobe zitiert (siehe Anhang).

Buch und Leseprobe zeigen überdies erstmals, daß die enorm verbesserten empirischen Beobachtungen mit Großteleskopen, Raumsonden, extrem genauen Uhren u.a. die Theorie stark vereinfacht haben.
Es wurde vor allem

A) die Allgemeine Relativitätstheorie befreit vom bisherigen Zwang, das Prinzip von Energie-Erhaltung aufzugeben und

B) empirisch unprüfbaren Hypothesen der Boden entzogen.      

Dieses Buch füllt eine Lücke, denn auch unter hervorragenden Darstellungen über Gravitation konnte ich keine finden, die empirisch gesichertes Wissen von Hypothesen klar abgrenzt. Das Buch ist gedacht für (auch diesbezüglich) anspruchsvolle Astronomen, Kosmologen, Physiker, Studierende und Laien.

Hypothesen als Ersatz für fehlende eigene Phantasie? Ich leide ja gar nicht an fehlender Phantasie. Was mir fehlt ist Wissen. Was wissen wir wirklich? Das ist die Frage dieses Buches. Wenn man ein Leben lang gewohnt ist, zu fragen, vor allem selbstkritisch, dann findet man vielleicht ab und zu Neues, aber noch erstaunlicher, man findet etwas anderes als das, wonach man gesucht hat. So ging es mir mit Gravitation. Nicht Phantasien haben sich erfüllt, die Wirklichkeit zeigte sich faszinierender als die an ihrer Statt gedachten Hypothesen. Eine Erfahrung dürfte den Leser ebenso überraschen wie mich, nämlich welche Fülle von nie geahnten Erkenntnissen wir gewinnen, wenn wir die Welt ohne das Filter von
Hypothesen betrachten, wenn wir also zunächst von der heute von allen Physikern anerkannten Physik ausgehen, insbesondere von der Speziellen Relativität, und wenn wir Autoritäten daran messen, ob sie einen Dialog mit uns führen können, das heißt, ob sie, statt nur ihr Bild von der Welt zu wiederholen, dem Leser die Kunst lehren, selbständig kritisch zu denken ohne sich auf Autoritäten zu berufen.

Für Aufdeckung eines grundsätzlichen Fehlers in diesem Buch ist ein Preis von 25000  ausgesetzt.

Rudolf Kießlinger

Wenn Leser diesen Text an Interessierte weiterschicken (oder mir Adressen mitteilen), dann könnte es gelingen, den Boykott zu durchbrechen, den zu viele Redaktionen wissenschaftlicher Journale gegen jene Wissenschaftler verhängt haben, die kritisch zu den Hypothesen vom Urknall (und oft auch zu Schwarzen Löchern) sind. Das sind viele hervorragende Wissenschaftler, u. a.
Fred Hoyle (gestorben 2001), H. C. Arp, G. Burbidge, J. Narlikar, Th. Gold, H. Bondi (ehemaliger Direktor von ESA, Verfasser von "Einsteins Einmaleins", eine der besten, dazu leicht verständlichen Einführungen in die Relativitätstheorie). Hoyle trat als Präsident der Royal Astronomical Society wegen der Anfeindungen zurück.

Ich war völlig überrascht, als ich auf einen Text, der diese Kritiker bestätigt, von einigen Redaktionen feindselige (oder gar keine) Antwort erhielt, denn ich hatte keine Ahnung, daß ein solcher mir unerklärlicher Boykott wie im Mittelalter heute überhaupt möglich ist.

 

 

 

 

 

1 Haben Sie das gewußt?

Diese Frage an den Leser bezieht sich auf bisher unbeachtete Ergebnisse der folgenden oft zitierten Messungen:

1.     Rotverschiebung entfernter Galaxien mit sämtlichen Voraussetzungen auch für den folgenden Text.

2.     Messung des Gravitations-Dopplereffektes, das ist die von Einstein richtig vorausgesagte Abnahme der
Frequenz des Lichts bei Abstrahlung gegen das Schwerefeld.

Vorweg sei betont, daß nichts Neues vorausgesetzt wird. Neu ist nur die Verknüpfung bisher beziehungslos verstreuter theoretischer Ergebnisse, die allgemein anerkannt und durch Messungen bestätigt sind.

Beachten Sie bitte, daß  keine zusätzlichen Hypothesen oder Annahmen gemacht werden.

1.1       Erklärung der Rotverschiebung ferner Galaxien

Im Jahre 1971 erregte ein von J. C. Hafele und R. Keating [Science 177, 166 (1972) ] durchgeführtes Uhrenexperiment weltweit Aufsehen. Es bestätigte erstmals experimentell die berühmte Voraussage der Allgemeinen Relativitätstheorie, wonach sich bei Annäherung an das Gravitationszentrum, also bei Verringerung der Höhe bezüglich Meeresniveau, der Gang von Uhren verlangsamt. Die Messung wurde seitdem mit steigender Genauigkeit bestätigt. Die Verlangsamung des Zeitablaufs ist unabhängig von der Art der Uhr. Gemessen wurde mit Atomuhren. Atome sind Uhren, denn nach der relativistischen Zeitdefinition ist jede atomare Eigenfrequenz ein idealer Taktgeber für die Zeitmessung.

Je stärker das Gravitationsfeld, umso langsamer verstreicht die Zeit. Behauptet wird nun folgendes:

Während bisher angenommen wurde, die Rotverschiebung entfernter Galaxien würde deren „Flucht“ beweisen, ergibt sich aus der Abhängigkeit des Zeitverlaufs vom Gravitationsfeld, daß das Licht entfernter Galaxien ohne Expansion  rotverschoben ist. Damit nicht der geringste Verdacht aufkommt, hier werde gemogelt, werden OHNE neue Hypothesen zum Beweis NUR solche Voraussetzungen gemacht, die von allen möglichen Kritikern und auch von Einstein anerkannt sind. Sie gelten für alles Folgende:

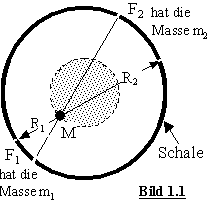
1.       Eine kugelsymmetrische Masse wirkt nach außen gravitativ so, als wäre ihre Masse im Mittelpunkt.

2.       Im Inneren einer Kugel nimmt die Gravitation zum Zentrum linear bis Null ab. Beweis siehe unten.

3.       Kosmologisches Grundprinzip:        
Jeder Punkt im Universum ist gleichberechtigt, kein Punkt ist ausgezeichnet. Das heißt: Jeder Punkt ist Mittelpunkt, keiner ist Randpunkt (so wie jedes Land der Erde „Reich der Mitte“ ist).

4.       Relativistisches Grundprinzip: Uhren in verschiedenen Bezugssystemen gehen verschieden schnell. Der Zeitablauf innerhalb eines Bezugssystems ist überall gleich, aber er ist (meßbar) verschieden zwischen verschiedenen Bezugssystemen, wenn sie sich a) relativ zueinander bewegen, aber auch, wenn in ihnen, nach Einstein, b) verschieden starke Gravitationsfelder herrschen.   
Je stärker das Gravitationsfeld, umso langsamer verstreicht die Zeit.

5.      

M und m sind die Massen in einem Zwei-Körper-System. (G = Gravitations-Konstante,   R = Abstand der Massen.)

Genaue Zeitmessung durch Vergleich mit der Dauer einer atomaren Resonanz Schwingung.

6.       Anziehungskraft 

Beweis zu Punkt 2:                       Wie stark wird eine Masse M  im Inneren  einer Massekugel  von

den Massen der Schale außerhalb der inneren Kugel angezogen? Die bezüglich M gegenüberliegenden Teilmassen m1 und m2 der Schale sind proportional den Flächen F1 bzw. F2, deren jede dem Quadrat ihres Abstandes R1 bzw. R2 proportional ist. Die Anziehungskraft dieser Massen nimmt mit dem Quadrat ihres Abstandes von M ab, das ist genau so viel, wie die Masse auf F1 bzw. F2 zunimmt. Dadurch heben sich die Anziehungskräfte der je gegenüberliegenden Massen auf die Masse M gegenseitig auf. Im Inneren übt somit die Schale keine Gravitation auf M aus. Wohl aber wird M angezogen von der Masse, die innerhalb der getönt und strichliert gezeichneten Kugel ist. Außerdem läßt sich beweisen, daß nach dem Klassischen Gesetz die Gravitation einer

kugelsymmetrischen Masse so wirkt, als ob die gesamte Masse in ihrem Mittelpunkt wäre. Das gilt allerdings nur für den Bereich außerhalb der Oberfläche der Kugel. Dringt jedoch eine fallende Masse in die kugelförmige Masse ein bis zu einem Abstand R_innen , der kleiner ist als der Radius R_o der Kugel, dann wirkt nur die Masse der konzentrischen Innenkugel mit dem kleinen Radius R_innen gravitativ auf sie, nicht aber die Masse der Kugelschale zwischen R_innen und R_o (was schon Newton erkannte). Wäre z.B. die Zentralmasse eine Hohlkugel, dann ist die Gravitation im Hohlraum Null. Nur außerhalb wirkt jede Schale wie eine Kugel, das heißt so, als wäre ihre Masse im Mittelpunkt vereinigt. [Siehe Kap. 3.9, Seite 35). (So haben übrigens Cavendish und Priestley 1771 das später nach Coulomb benannte Gesetz e₁ e₂ /R² für elektrostatische Anziehung  bewiesen.).

Überträgt man diese Überlegung auf die Massen des ganzen Universums, dann ist die Rechnung
besonders einfach wegen des fundamentalen kosmologischen Prinzips, daß es keinen ausgezeichneten Ort im Universum gibt. Jeder Punkt ist gleichberechtigter Mittelpunkt, keiner Randpunkt, leicht zu verstehen in Analogie zur Kugeloberfläche der Erde. Die Chinesen nennen ihr Land „Reich der Mitte“. Doch „Reich der Mitte“ ist jedes Land, denn in der Kugeloberfläche ist jeder Punkt „Mittelpunkt“,
keiner Randpunkt, obwohl der Flächeninhalt begrenzt ist. Das gilt auch für den Raum. Hat er eine in sich geschlossene Krümmung, so ist die Analogie offenkundig, sie ist aber auch offenkundig, wenn der Raum unbegrenzt ist und deshalb keine Oberfläche hat.

Universum als „Kugel“: Nun sei M eine ferne Galaxis. Ihre Distanz zu uns sei R_innen. Denken Sie sich bitte mit diesem Radius eine riesige Kugel aus dem Universum so ausgeschnitten, daß der Mittelpunkt bei uns und die beobachtete Galaxis auf ihrer Oberfläche ist. Alle von der Kugel umschlossenen Galaxien wirken auf diese ferne Galaxis M gravitativ so, als ob sie im Mittelpunkt der Kugel konzentriert wären. Das heißt konzentriert bei uns auf der Erde. Alle außerhalb dieser Kugel befindlichen Himmelsobjekte gehören zur „Schale“, haben also keine gravitative Wirkung auf die Galaxis in ihrer Oberfläche.

Aus der durchschnittlichen Massendichte des Universums berechnen wir die Masse der Innenkugel (Volumen mal Dichte) und daraus deren Gravitationskraft K auf die von uns betrachtete Galaxis. Diese Kraft ist das Maß für die Gravitation, die am Ort dieser Galaxis aus unserer Sicht herrscht.

„Aus unserer Sicht“ heißt, Gravitation ist eine relative Größe, Betrag und Richtung sind abhängig vom Standpunkt des Beobachters. Z.B. ist für frei fallende Beobachter die Gravitation an jedem Ort Null (z.B. Flugzeuglabor im Sturzflug). Ist ein Beobachter von der Galaxis weiter entfernt als wir, dann ist, aus seiner Sicht, die Gravitation, die er für den Ort der Galaxis mißt, größer, trotz des größeren Abstandes, denn die Gravitation nimmt zwar mit der zweiten Potenz des Abstandes ab, aber die gravitative Masse wächst mit dem Volumen, also stärker, eben mit der dritten Potenz des Abstandes (mit R³).

Die aus unserer Sicht mit dem Abstand wachsende Gravitation bewirkt die beobachtete Rotverschiebung weit entfernter Galaxien. So einfach ist die Rotverschiebung erklärt, ohne Expansion, ohne Urknall. Die Annahme eines Urknalls ohne Expansion wäre ein Widerspruch in sich.

Das Licht ist also bereits bei dessen Emission rotverschoben (im folgenden Kapitel „Der Gravitations-Dopplereffekt“ wird gezeigt, daß Licht von Gravitation gar nicht verändert werden kann).

Würden Raum oder Galaxienabstände expandieren, dann müßten wir eine weit größere Rotverschiebung messen, was nicht der Fall ist. Aber H.C. Arp und andere haben bei sorgfältigen Messungen mit Großteleskopen (auf die auch Fred Hoyle und andere seit mehr als 20 Jahren hinweisen) Rotverschiebungen entdeckt, die durch Fluchtgeschwindigkeit nicht, wohl aber mit dieser gravitativen, von der Entfernung abhängigen Rotverschiebung erklärbar sind. Davon unabhängig entsteht am Ort der Lichtquelle eine zusätzliche Rotverschiebung durch örtliche Gravitationsfelder stellarer oder galaktischer Massen oder durch Felder der extrem konzentrierten Massen von Quasaren. Mit derartigen Beobachtungen hat vor allen H.C. Arp Pionierarbeit geleistet.

Denken wir uns einen Beobachtungspunkt, der am Zusammenfallen des Universums nicht teilnimmt und von dem wir als ruhende Zuschauer das Zusammenfallen betrachten. Im Lauf des Fallens haben die Massen fast Lichtgeschwindigkeit erreicht. Während sich ihre Abstände verringern, verkürzt sich zugleich infolge der großen Geschwindigkeit erstens der Längenmaßstab, mit dem diese Abstände (in jeder Richtung!) gemessen werden, und zweitens ändert sich mit dem gleichen Faktor aus unserer Sicht der Zeitmaßstab. Sobald nun ihre Abstände gerade so viel kleiner werden als sich der Längenmaßstab relativistisch verkürzt, messen wir von unserem Standpunkt überhaupt keine Veränderung der Distanzen mehr, weil sich beide Veränderungen kompensieren. Die Frage ist nur, ob es einen solchen Beobachterstandpunkt gibt. Es gibt ihn, es ist der „Mittelpunkt“, in dem sich nach einem kosmologischen Prinzip jeder Beobachter im Universum befindet. Würden die zusammenfallenden Massen diesen Punkt erreichen, dann hätten sie Lichtgeschwindigkeit, aber dazu bräuchten sie unendliche Zeit.

Das ergibt die scheinbar paradoxe Situation, daß das Universum durch seine eigene Gravitation in sich zusammenfällt und dennoch alle Massen relativ zueinander in Ruhe bleiben. Das liegt also daran, daß zugleich mit dem Schrumpfen des Universums alle Maßstäbe im selben Verhältnis schrumpfen. Es verbleiben nur kleinere Individualgeschwindigkeiten, die einzelne Massen relativ zueinander haben können, z.B. infolge ihrer lokalen Gravitation. Das Einzige, was am Zusammenfallen wahrnehmbar ist, ist die Verlangsamung des Zeitablaufs relativ zu jedem vorangegangenen Zustand, bei dem das Universum größer gewesen ist. Das Licht, das uns von weit entfernten Galaxien nach langer Zeit erreicht, ist uralt. Zur Zeit seiner Emission war das Universum mit allen Maßstäben größer. Da wir alle Maßstäbe durch das Licht definieren, ist die Wellenlänge des Lichts der einzig mögliche Längenmaßstab. Also muß in früherer Zeit die Lichtwellenlänge um ebensoviel größer gewesen sein wie das Universum größer war. Das heißt, jedes fossile Licht ist rotverschoben, und zwar umso mehr, je größer Entfernung und Zeitdistanz zur Lichtquelle. Das begründet einmal mehr die Rotverschiebung fossilen Lichtes.

Nun die zweite berühmte Messung. Sie beruht auf den gleichen physikalischen Prinzipien:

1.2 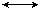      Der Gravitations-Dopplereffekt

Pound und Rebka konnten 1960 mit Hilfe des Mößbauer-Effektes die Frequenzänderung des Lichts im Gravitationsfeld messen.

Sie zeigten, daß die Energie (Frequenz) z.B. von Gammastrahlen, die von der Basis des Turms aufsteigen, abnimmt, und zwar mit der Energiedifferenz Dj/c², die Einstein vorausgesagt hat. Darin ist Dj die Zunahme der Potentiellen Energie beim Besteigen des Turms, Dj/c² ist die Masse dieser Energiedifferenz (alle Größen pro Masseneinheit!).

Nach üblicher Erklärung erhalten umgekehrt einfallende Photonen Energie aus dem
Gravitationsfeld. Für Photonen, die ja nur kinetische Energie haben, gelte also dasselbe wie für fallende Körper, denn die würden ihre
kinetische Energie ja ebenfalls aus dem Feld beziehen. Doch diese verbreitete Erklärung ist falsch. Es gilt vielmehr folgende Behauptung.

Die Photonenenergie (d.h. die Frequenz!) wird vom Gravitationsfeld nicht verändert.

Deshalb können Photonen aus jedem beliebigen Schwerefeld ohne Energieeinbuße entweichen, als ob es das Feld nicht gäbe. Übrigens schließt das die Möglichkeit Schwarzer Löcher aus.

Diese Behauptung treibt die Vertreter der bisherigen Theorie auf die Barrikaden, aber sie läßt sich
mühelos beweisen und verstehen mit einer anderen Entdeckung Einsteins, und zwar wie folgt:

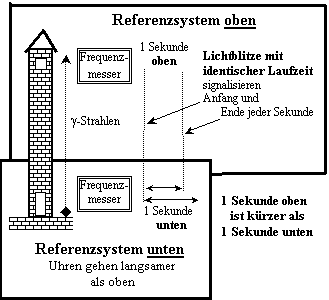
Nach Einstein verstreicht die Zeit unten mit dem Faktor 1+Dj/c² langsamer als oben. Das wurde ab 1971 mit steigender Genauigkeit gemessen (Hafele & Keating 1971, University of Maryland 1976 u.a.). Das heißt: Die Sekunde dauert unten länger als oben – eben um den Faktor 1+Dj/c². Wenn (und nur wenn) die Frequenz sich nicht ändert werden pro Sekunde um genau so viel mehr Schwingungen gezählt, wie die Sekunde länger dauert. Das wurde gemessen. Es beweist, daß die Frequenz der Gammastrahlen unten und oben gleich ist. Daß man unten genau eine mit diesem Faktor erhöhte Frequenz mißt, liegt also daran, daß die innere Uhr des unteren Frequenzmessers dem im unteren Referenzsystem geltenden langsameren Gang der Zeit folgt. Der bisherige Gedankenfehler bestand darin, daß man Meßwerte aus dem oberen mit denen des unteren Referenzsystems verglich, ohne sie vorher auf das gleiche Referenzsystem umzurechnen.

Hier nun fiel mir ein Verteidiger von Urknall und Schwarzen Löchern ins Wort. Er sagte, beide Frequenzmesser wären im gleichen Referenzsystem, weil es prinzipiell unmöglich sei, ihre Uhren zu synchronisieren. Wenn der Unterschied des Gravitationsfeldes für jeden Ort andere Meßwerte für Raum- und Zeit ergibt, dann doch im gleichen Referenzsystem. Daraus sei zu folgern, daß die Frequenzen wirklich verschieden sind. Doch die behauptete Unmöglichkeit der Uhrensynchronisation ist ein Irrtum.

John Archibald Wheeler, ein Hauptvertreter der Theorie Schwarzer Löcher, synchronisiert z.B. die
Uhren, indem der obere Frequenzmesser Anfang und Ende jeder Sekunde durch Lichtblitze signalisiert¹.

Ein Referenzsystem ist definiert durch Synchronisation ruhender Uhren an allen Orten. Eicht man den unteren Frequenzmesser mit diesen Sekundensignalen von oben, dann mißt man für die Gammastrahlen oben und unten die gleiche Frequenz. (Laufzeit und Frequenz der Lichtblitze sind ohne Einfluß, denn sie durchlaufen stets die gleiche Turmhöhe, egal, ob zu Anfang oder zu Ende jeder Sekunde.)

Schlampige Definition des Beobachterstandpunktes findet sich in unzähligen Arbeiten über die Relativitätstheorie und führt zu heute ritualisierten Fehlschlüssen, z.B. zum verbissen verteidigten Urknall.

Zu erwähnen bleibt, daß ein unten emittiertes Photon aus einem Atom geringerer Masse kommt. Deshalb ist dessen Frequenz bereits bei der Emission niedriger, also schon vor dem Aufsteigen im Feld.

Die Referenzsysteme der beiden Frequenzmesser kann also derjenige problemlos unterscheiden und auch umrechnen, der physikalisch argumentiert statt mit dem Vorwurf eines Widerspruchs zu Einstein.

Doch der Kritiker fühlt sich falsch gedeutet. Er behauptet, daß man den unteren Frequenzmesser nicht mit der Sekunde des oberen Freuenzmessers eichen dürfe. Er sagt, man könne und dürfe das oben
abgestrahlte Licht unten nur mit dem unveränderten unteren Frequenzmesser messen, und dann mißt man eben unten eine höhere Frequenz, das zeige die Theorie und die Messung. Damit sei bewiesen, daß das Licht Energie aus dem Feld gewonnen habe.

Aber da hat sich der Kritiker eine harte Nuß eingehandelt. Niemand wird bestreiten, daß die Sekunde des oberen Frequenzmessers durch eine genau definierte Anzahl von Atomschwingungen, z. B. der des Cäsiums, geeicht ist, eingebaut im Frequenzmesser. Nun denke man von oben einen einzigen Impuls abgestrahlt mit genau der Anzahl von Schwingungen, die 1 Sekunde definiert (definiert mit dieser
Frequenz des Cäsiumatoms). Vorher werde ein identischer Frequenzmesser von oben nach unten gebracht mitsamt seinen Cäsium-Eich-Atomen. Dieser kann unabhängig vom Gravitationsfeld unten nichts anderes messen als den einen Impuls, der unten natürlich die gleiche Anzahl von Schwingungen hat wie oben. Was also mißt der untere Frequenzmesser, dessen Sekunde mit der gleichen Schwingungszahl geeicht ist? Er kann nichts anderes messen als die Anzahl der Schwingungen dieses einen Impulses, die sich unten genau so auf 1 Sekunde verteilen wie oben, eben weil die Sekundendauer oben und unten exakt gleich definiert ist.

Wie will nun der Kritiker erklären, daß man dennoch und von ihm unbestritten unten eine höhere
Frequenz mißt, was ja sein Argument ist? Er könnte höchstens noch postulieren, daß nur die erste Schwingung mit Lichtgeschwindigkeit nach unten läuft, jede folgende aber schneller als Licht, wodurch unten die letzte Schwingung ankommt bevor die Sekunde zu Ende geht. Dann verbliebe bis zum Ende der Sekunde eine Pause, in der weitere Schwingungen Platz hätten.

Erklärbar ist die Messung der Frequenzerhöhung (mit dem Faktor 1+Dj/c²) nur mit dem Energie-erhaltenden Gravitationsgesetz, das aus diesen Messungen ableitbar ist, wie nun gezeigt wird.

________________________________________________________

1)   Der Vorschlag, die Uhren durch Lichtsignale zu synchronisieren, findet sich in „Gravitation und Raumzeit“ von John Archibald Wheeler (Spektrum Verlag 1989) auf Seite 174. In anderen Schriften von Weeler findet sich auch die Feststellung, daß sich Massen im Schwerefeld ändern, nur wurde dies in der Theorie der Schwarzen Löcher nicht berücksichtigt.

 

1.3       Das Energie-erhaltende Gravitationsgesetz

Sich des Problems der Energieerhaltung im Gravitationsgeschehen bewußt hielt Newton eine Erweiterung seines Gesetzes für notwendig und möglich, denn er empfahl dazu weitere Forschung. Aber erst mit Einsteins genialer Entdeckung der Äquivalenz von Masse und Energie läßt sich Energie-Erhaltung in das Gravitationsgesetz einbeziehen. Das wäre schon mit der Relativitätstheorie seit 1905 möglich gewesen. Schwer zu begreifen, warum das, soweit mir bekannt, fast ein Jahrhundert lang nie versucht worden ist (ausgenommen von E. Milne, aber nur für die Hypothese der Expansion des Universums).

Um die Ableitung überzeugender zu machen gehe ich von den oben genannten Messungen aus. Wem die Differentialrechnung weniger liegt kann die jetzt folgende Ableitung überschlagen. Er muß dann eben dem Resultat vertrauen. In den ersten Kapiteln konnten wir feststellen, was heute allgemein akzeptiert ist:

Wenn sich die Gravitationskraft erhöht (z.B. bei Annäherung an eine Zentralmasse), so verstreicht die Zeit langsamer, das heißt: Je stärker das Gravitationsfeld umso langsamer gehen die Uhren.

Atome sind Uhren, denn jede atomare Eigenfrequenz kann als Taktgeber für die Zeitmessung dienen. Extrem wichtig ist nun Folgendes: Die atomaren Eigenfrequenzen sind proportional der Atommasse.

Verlangsamung der atomaren Eigenschwingung bedeutet, daß die Masse des Atoms mit dem gleichen Faktor abnimmt, allerdings, wie erst später erklärt wird, relativistisch, das heißt nur aus Sicht eines im Ausgangspunkt zurückbleibenden Beobachters. Das folgt aus dem Uhrenexperiment von Hafele und Keating. Deshalb muß, aus Sicht dieses Beobachters, eine fallende Masse und damit ihre Gravitationskraft mit dem Faktor 1–Dj/c² abnehmen. Dj ist die Potentialabnahme. Weil die kinetische Energie pro Masseneinheit um dieses Dj zunimmt, ist also die Masse selbst die Quelle der Potentiellen Energie, nicht das Feld der Zentralmasse. Ihre Anfangsenergie bei R= ¥ ist mc². Um das zu formulieren multiplizieren wir m mit einen positiven Faktor f(R), der kleiner als 1 und zu berechnen ist. Es verbleibt mf(R).

Vorausgesetzt sei der einfachste Fall, ein System aus nur zwei Körpern, m fällt auf M. Der Beobachter sei auf der (zunächst unbewegt angenommenen) Masse M.

Der Abstand R ist relativistisch definiert durch die Laufzeit des Lichts. Im Unendlichen ist die

(1.1)    gesamte potentielle Energie = (M+m)c². Davon verbleibt im Abstand R aus der Sicht von M:

(1.2)    E_pot = [M+m×f(R)]c²  mit 0 < f(R) < 1.

Wegen  E_kin = ||   und   E_pot = (M+m)c²– E_kin     ist die Ableitung nach R, also die

Energieumwandlung E_pot in E_kin pro Einheit des Weges R

(1.3)    |K| = || = mc²×f ¢(R).   Diese „Energie pro Wegeinheit“ heißt „Gravitationskraft“.

Wenn unter Beibehaltung des Newtonschen Gravitationsgesetzes die „Masse“ durch ihre gravitative Funktion definiert wird, dann ist mf(R) ihr Betrag. Die gravitative Masse mf ist also nicht länger eine Konstante. Für relativistische Denkweise ist das nichts Ungewöhnliches, die Masse m ist ja auch als verschieden erkannt für unterschiedlich bewegte Beobachter. Newtons Kraftgesetz lautet dann

(1.4)    K = G  und E_pot = (M+m)c² –,  also |K|= ||.  Gl.(1.4) = Gl.(1.3) liefert:

            G = mc²×f ¢(R),   anders geordnet:      Die linke Seite

ist die Ableitung von lnf(R), die Integration der rechten Seite ergibt   –

Somit ist bei Integration von ¥ bis R:   lnf = –.  Dies als Exponent der Basis e ergibt

Symmetrie der Massen M und m:

Im Kapitel 3.3 Seite 23 wird dazu ergänzend der Beweis geführt, daß für den Abstand R der Massen immer der Abstand zum gemeinsamen Schwerpunkt gemeint ist. Dann nimmt auch die Zentralmasse M ab, auch mit dem Faktor – e^–a/R, nur ist für sie die Größe a = Gm/c² statt GM/c². Setzt man aber doch den vollen Abstand der beiden Massen ein, dann muß für a im Exponenten a = G(M+m)/c² stehen.
Das macht die Formel in beiden Massen symmetrisch.

1.4       Kurvenverlauf

Sie werden mein Erstaunen nachvollziehen, wenn sich nun schrittweise herausstellt, daß allein diese Anpassung an die Spezielle Relativität die Klassische Theorie in die Allgemeine Relativitätstheorie verwandelt, aber ohne Feldenergien außerhalb der Masse im gekrümmten Raum! Damit entfällt die Hypothese von Einstein und Newton, daß der „leere Raum“, also das Vakuum, eine Energiequelle sei.

Klassisches Gesetz (normiert)   Schwarzschild     Radius   0      0,5      1              2        Abstand R/a   1 0   Kraft K/Kmax

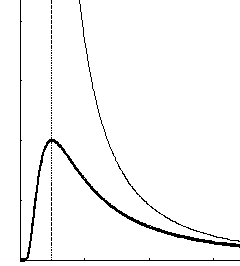
Das Diagramm zeigt die Gravitationskraft für den Fall, daß sich die Massen extrem nahe kommen. Dazu müßten sie fast punktförmig sein. (Der Abstand R ist in Vielfachen von a angegeben, 2a ist der sogenannte Schwarzschildradius. Für die Sonnenmasse M ist z.B. a = 1484 Meter). Für größere Abstände nähern sich die beiden Kurven einander asymptotisch so sehr, daß sie praktisch zusammenfallen. Das ist der Grund, warum sich die relativistischen von den klassischen Bahnen der Himmelskörper fast nicht unterscheiden. Auch wenn sich beliebig große Massen extrem nahe kommen entsteht kein Schwarzes Loch, weil dann die Gravitation viel kleiner ist als nach Newton und zuletzt ganz verschwindet. Aber sie prallen zusammen. Das führt zu extremer Wärmeentwicklung und damit zur vollständigen Zerstrahlung der Energie in dieser größten im Universum möglichen Explosion (Gamma-Burst).

Bild 1.3 Gravitationskraft (alle Kurven normiert auf K/K_max). Siehe auch die Diagramme auf Seite 83

Die Differenz zwischen dem Klassischen Gesetz und der Energie-erhaltenden Gravitation spiegelt genau die Umwandlung von Potentieller in Kinetische Energie wieder. Das sei im Folgenden noch eindrucksvoller an den Formeln demonstriert. Auf S.84 findet der Leser eine Diskussion dieser Kurve.

1.5        „Der kleine Unterschied“ zu Klassischer und zu Einsteins Theorie

Aus dem der Klassischen Potentialtheorie übernommenen Postulat, daß die Gravitationsenergie quellenfrei im „leeren Raum“ entsteht, schuf Einstein seine berühmten Feldgleichungen. Danach ist durch das Gravitationsfeld einer Zentralmasse M der Zeitmaßstab t in unendlicher Entfernung kürzer, verglichen mit t_o im Abstand R. Zunächst zitiere ich hier für das Quadrat eines Zeitintervalls t die

(1.10) Einsteinsche Formel   = .   (G = Gravitationskonstante)

Es sieht so aus, als ob diese Formel mathematisch zwangsläufig wäre, doch sie ist intuitiv postuliert. Einstein beweist sogar, daß sie aus nichts ableitbar ist. Diese geniale Intuition fußt auf dem Postulat der Quellenfreiheit des Gravitationsfeldes. Das Intervall läßt sich auch anders postulieren, die Folge wäre eine andere Theorie. Doch das von Einstein durch diese Formel postulierte Intervall erwies sich als Geniestreich und war so fruchtbar und überzeugend, daß in den rund acht Jahrzehnten bis heute jeder Zweifel daran als geradezu unsinnig verworfen wurde.

Nach Energie-erhaltender Gravitation kann aber der Zeitmaßstab weder so noch überhaupt postuliert werden, denn er liegt bereits fest, und zwar anders als Einstein dachte. Wie zu Gl.(1.7) gezeigt, ändern sich Masse und Zeit notwendig mit dem gleichen Faktor. Uhren können prinzipiell mit jeder Spektralfrequenz eines Atoms gesteuert werden. Spektralfrequenzen sind atomaren Energiesprüngen proportional, das sind Massenänderungen. Somit ist jede atomare Masse immer auch eine mit dem Gang der Zeit synchron gehende Uhr. Jede Änderung e^–a/R der Masse gilt auch für den Zeitablauf. Ein Zeitintervall t_o im Abstand R von der Masse M war also im unendlichen Abstand kürzer, nämlich t = t_oe^–a/R.

(1.11)

Um dieses Intervall vergleichen zu können mit dem von Einstein postulierten Quadrat des Zeitmaßstabs sei die Formel quadriert, t² = e^–2a/R, und dann in eine Reihe entwickelt. Unter die Reihe schreibe ich zum Vergleich Newtons Axiom der absoluten Zeit sowie Einsteins hypothetischen Zeitmaßstab:

123      ­Newtons Axiom- - - -enthält nur das konstante 1.Glied  (Zeit und Masse sind absolut           und von Gravitation unabhängig)

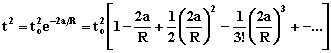 =  Quadrat des Intervalls. Zum Vergleich:

14243          ­Einsteins Hypothese- - - bricht nach dem 2.Glied ab (Schwarzes Loch bei R = 2a)             Zeit zu stark verkürzt, Masse zu wenig.

1.Näherung:

1444444244444443        Energie-erhaltende Gravitation - enthält alle Glieder (kein Schwarzes Loch),                Masse und Zeit ändern sich im Gravitationsfeld mit dem gleichen Faktor

_2.Näherung:

3.Gemessen aber wurde:

Auf einen Blick ist erkennbar, warum sich die drei Theorien dem gleichen exakten Resultat annähern müssen, wenn durch Einbeziehung vernachlässigter Glieder Abweichungen schrittweise verschwinden.

1. Newtons absoluter Gang der Zeit ergibt sich, wenn die Reihe nach dem konstanten 1. Glied abgebrochen wird. Dann ist t = t_o, Newtons Zeit ist unabhängig vom Abstand R zum Gravitationszentrum.

2. Das von Einstein postulierte Intervall entsteht durch Hinzunahme des negativen zweiten Gliedes
–2a/R.   Für R >> 2a = 2GM/c² ist dieses Glied extrem klein. Für die Sonnenmasse ist 2a @ 3 km, der Abstand R zur Erde ist 150 Millionen km. Deshalb liefert Einsteins Allgemeine Relativitätstheorie praktisch die gleichen Plantenbahnen wie das äußerst genaue Newtonsche Gesetz. Die gerade noch meßbare Abweichung vom Newtonschen Gesetz konnte als glänzende Bestätigung für Einsteins Postulat des Intervalls gedeutet werden. Nichts ließ vernachlässigte Glieder höherer Potenz vermuten, da diese um viele Zehnerpotenzen unter der Meßgenauigkeit von planetarischen Umlaufszeiten liegen. (Die den Umlaufzeiten überlagerten sehr viel größeren Störungen setzen der Meßgenauigkeit Grenzen.)

Unterschiede treten erst auf in der Nähe des sogenannten Schwarzschild-Radius R_S = 2a.  Ist R = R_S, dann ergibt Einsteins Formel t = t_o(1– 2a/2a) = 0, die Zeit steht still. Damit folgt aus t_o= 0 daß bei R = R_S > 0 die Entweichgeschwindigkeit v = c ist, Kennzeichen für ein „Schwarzes Loch“.

3. Werden jedoch nach dem Energie-erhaltenden Gravitationsgesetz die restlichen Reihenglieder nicht vernachlässigt, dann gilt  t = t_oe^–a/R > 0  für alle R > 0, und nur für R = 0 ist die Zeit t = 0 und v = c.
Aber R = 0 bedeutet, daß es kein Schwarzes Loch gibt.

Außerdem wird bei Einstein die Raumgeometrie verzerrt, denn wenn bei endlichem Abstand R_S > 0 alle Zeitabstände verschwinden, dann müssen auch räumliche Abstände mit dem gleichen Faktor verschwinden, weil für Licht der Quotient beider stets die unveränderliche Lichtgeschwindigkeit c sein muß.

Folgerungen

Aus der Fülle von Folgerungen aus Energie-erhaltender Gravitation seien diese für einen ersten Überblick zunächst nur kurz erläutert. Ausführliche Ableitungen finden sich in den folgenden Kapiteln. So wird schrittweise erkennbar, daß der mit Gl.(1.5) bis (1.9) definierte Massenbegriff deckungsgleich ist sowohl mit allen Beobachtungen bewegter Massen als auch mit allen bekannten meßbaren Ergebnissen der Allgemeinen Relativitätstheorie. Da Einführung von Energieerhaltung die Quellenfreiheit des Feldes aufhebt, weichen zwar die Formeln von Einsteins Relativitätstheorie ab, aber nur durch den Faktor e^–a/R, der sich für R >> a von 1 nicht unterscheiden läßt. Die Abweichungen dominieren aber, wenn R der sehr kleinen Länge 2a nahekommt. Bei wesentlich größeren Abständen sind viele Formeln oft dieselben wie bei Einstein oder auch wie in der Klassischen Theorie. Bei Differentiation bleibt e^–a/R erhalten.

1.6       Relativistische Bahnen der Himmelskörper,
Lichtablenkung an großen Massen

Es waren vor allem zwei Argumente, welche die Physiker von der Einsteinschen Allgemeinen Relativitätstheorie überzeugten. Zunächst konnte Einstein mit dem oben zitierten Postulat [Gl.(1.10)]

des Zeitintervalls  =                      (G = Gravitationskonstante)

die mit dem klassischen Gesetz nicht erklärbare Drehung der Bahnellipse des Merkur theoretisch
begründen. Damit konkurrierte er allerdings mit anderen Erklärungsversuchen, aber der Durchbruch zugunsten der Einsteinschen Theorie war die mit keiner anderen Theorie erklärbare Ablenkung des Lichtes im Gravitationsfeld der Sonne. Für diese erhielt er in Übereinstimmung mit der Messung einen Winkel, der doppelt so groß war wie nach der Klassischen Theorie.

Führt man jetzt die gleichen Rechnungen mit dem Energieerhaltenden Gravitationsgesetz durch, so
erhält man die gleichen Formeln wie Einstein, aber auf sehr viel einfachere Weise, und dies sowohl für die sogenannte „Periheldrehung“ der Bahnellipsen als auch für die Lichtablenkung an großen Massen.

Daraus folgt übrigens eine Erkenntnis, die den Abhandlungen zur Einsteinschen Theorie schwer zu entnehmen ist. Diese betrifft die Gestalt des Gravitationsfeldes. Nach der Speziellen Relativitätstheorie sind Masse und Energie einander „äquivalent“, das heißt: Jede Masse m ist zugleich Energie, nämlich
E = mc², und jede Energie E ist zugleich Masse,  m = E/c². Wählt man das Einheiten-System so, daß die Lichtgeschwindigkeit c = 1 wird, dann kann man E = m schreiben, was Einstein oft getan hat.

Ist die Energie in einem „Körper“ gebunden, so ist die Gestalt des Graviationsfeldes kein Problem.
Welche Gestalt aber hat das Gravitationsfeld der freien Energie, z.B. der kinetischen Energie?

Dazu muß man wissen, daß die Masse durch ihre Trägheit definiert ist, daß aber in der Speziellen Relativitätstheorie ein und derselbe Körper zwei verschiedene „träge Massen“ hat. Er hat, je nachdem, ob man ihn in Bewegungsrichtung oder quer zur Bewegung beschleunigt, eine „Longitudinale“ und eine „Transversale“ träge Masse, und die eine hat eine dreifach größere Differenz zur „Ruhemasse“ als die andere. Die Differenzenergie muß aber, wie jede Energie, ein Gravitationsfeld haben. Es müssen also von einem Körper zwei Graviationsfelder zugleich existieren. Wie ist das zu erklären? Falls es dazu
irgendwo eine Aussage gibt, dann jedenfalls so versteckt, daß sie kaum einem Physiker bewußt ist, wie man sich leicht durch Umfragen überzeugt.

Das Energie-erhaltende Gravitationsgesetz unterscheidet sich von der Einsteinschen Theorie allein darin, daß es die extremen Raumverzerrungen in der Nähe des Schwarzschildradius nicht enthält. Danach gibt es bei diesem Radius diese Einsteinsche Singularität nicht, bei der die fallende Masse Lichtgeschwindigkeit erreichen würde. Diese mathematisch extrem komplizierte Raumverzerrung verschwindet mit Einführung von Energieerhaltung. Das vereinfacht die mathematische Beschreibung drastisch, auch bei großen Abständen. Das Gravitationsgeschehen, das bisher ein Eigenleben hinter einer Festungsmauer aus abstrakten Begriffen führte, wird dann plötzlich für den Physiker durchschaubar, folgt also nicht länger einer nur formalen Logik, die ebenso schwer zu kontrollieren wie vorzustellen ist.

Zunächst wird klar, daß in der Relativitätstheorie die klassische Definition der Masse durch Trägheit nicht beibehalten werden kann, weil in der Relativitätstheorie beides schon definiert ist, die Masse durch Energie, und die Energie durch die Gravitation. Natürlich läßt sich die Reihenfolge der Definitionen umkehren, nur darf eine Größe wie z.B. die Masse nicht zweifach unterschiedlich definiert werden.

Mit Energie-Erhaltung läßt sich nun anschaulich zeigen, daß auch die kinetische Energie ein Gravitationsfeld hat, aber mit zwei unterschiedlichen Werten. Es ist Null in Bewegungsrichtung und dafür doppelt so groß quer zur Bewegung! In beiden Richtungen kommt noch das Feld der Energie dazu, die aufgewendet wurde, um den Körper auf die vorliegende Geschwindigkeit zu beschleunigen. Diese ist allerdings Null, wenn im Gravitationsfeld ein Körper seine Fall-Energie aus seiner eigenen Masse bezog.

Das sind Resultate, die für Physiker neu sind. (Herleitung in den Kapiteln 3.4+3.5, Seite 24‑27).

Angemerkt seien zwei Folgen der Richtungsabhängigkeit der Gravitation der kinetischen Energie:          
1. Die Periheldrehung der Planetenbahnen und 2. Die doppelte Lichtablenkung an großen Massen.
Für das Licht ist das unmittelbar klar, weil Licht nur kinetische Energie hat, deren Gravitation quer zur Bewegung doppelt so groß ist wie die fehlende Energiezunahme in Ausbreitungsrichtung. Nach der Klassischen Theorie hingegen müßte die Gravitation der kinetischen Energie kugelsymmetrisch sein

1.7       Der endliche Radius des Universums

Eine Überraschung ergibt sich, wenn man im Kugelmodell des Universums (beschrieben in Kapitel
1.1 Rotverschiebung entfernter Galaxien) die Gravitationskraft auf eine weit entfernte Galaxis
berechnet, so wie sie aus unserer Sicht erscheint. Nach dem klassischen Gravitationsgesetz würde die Gravitation mit unbegrenzt wachsendem Abstand linear bis ins Unbegrenzte wachsen. Nicht so mit Energie-erhaltender Gravitation nach Gleichung (1.9). Zwar steigt auch nach dieser Gleichung die
Gravitation bis in sehr große Entfernung ebenfalls so gut wie linear, aber dann wird der Anstieg immer flacher, erreicht bei einigen Milliarden Lichtjahren Entfernung ein Maximum und fällt danach asymptotisch gegen Null ab. (Berechnet im Kapitel 3.10, ab S. 36, Formel (3.56), Diagramm dazu S.83 unten.)

Es ist sinnvoll, die Entfernung bis zum Gravitationsmaximum als „Radius des Universums“ zu definieren. Sinnvoll deshalb, weil es kaum möglich ist, den Radius eines beliebigen Himmelskörpers auf andere Weise zu definieren. Große Himmelskörper sind gasförmig. Also steht man vor der Frage,
welche Radien nicht vorhandene „Oberflächen“ haben. Fällt eine Probemasse auf einen solchen Himmelskörper, dann „spürt“ sie zunächst mit der Annäherung wachsende Gravitation. Beim Eintauchen in die Zentralmasse erreicht die Gravitation bei einem bestimmten Abstand R ein Maximum und nimmt danach in Richtung zum Zentrum ab bis Null. Der Abstand, bei dem die Gravitationsbeschleunigung am größten ist, eignet sich als Definition des Radius, und so kann man auch den Radius des Universums als den Abstand von uns definieren, bei dem  aus unserer Sicht  die Gravitation am größten ist.

Macht man das, dann zeigt sich zunächst, daß der Radius R des Universums nur von dessen mittlerer Massendichte r abhängt, und zwar ist er (®Seite 38) proportional der reziproken Wurzel aus der Dichte

(3.58)              R =             (c = Lichtgeschwindigkeit, G = Gravitationskonstante).

Berechnet man die mittlere Dichte r aus der geschätzten Gesamtmasse aller sichtbaren Objekte am Himmel, dann erhält man r @ Masse eines Wasserstoffatoms pro Kubikmeter. Wenn man zusätzlich dunkle Materie annimmt, so ist die Dichte wesentlich größer. Schätzt man sie viermal so groß, dann ergibt die Rechnung für den Radius des Universums = 16 Milliarden Lichtjahre [mit Formel (1.9)]. Das entspricht ungefähr den heutigen Schätzungen bei Annahme eines expandierenden Universums.

1.8       Kosmologische Konsequenz:

Gravitation ist die Umkehrung des Entropiesatzes

Für Wärmeenergie gilt der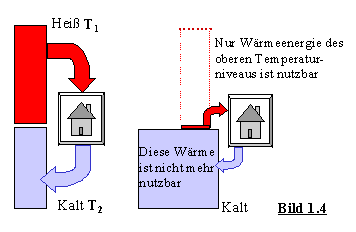

2. Hauptsatz der Thermodynamik:

In einem abgeschlossenen System läßt sich von der ganzen Wärmeenergie nur der Teil E als mechanische Energie gewinnen, der im Temperaturgefälle T₁ – T₂ steckt, nicht jedoch  die  Wärme  im  kältesten  Teil  T₂.

Somit ist der

aus Q  gewinnbare Energie-Anteil

(1.12)  (nach Carnot).

Daraus zog man eine kosmologische Konsequenz: Wenn sich in ferner Zukunft alle Sterne auf das tiefste Temperaturniveau abkühlen, dann stirbt das Universum den „Wärmetod“, weil es dann nirgends ein Temperaturgefälle gibt. Ohne Temperaturgefälle ist die Energie des untersten Niveaus auf keine Weise verfügbar. Leben wäre unmöglich.

Das Bild zeigt, daß auch die durch Lebewesen genutzte Energie zuletzt als Abwärme das unterste Temperaturniveau erreicht. Der „Wärmetod der Welt“ bleibt für immer bestehen. Natürlich gab es Zweifel, ob der 2.Hauptsatz der Wärmelehre auch für kosmische Prozesse und Zeiten wirklich gilt.

Mit dem Energieerhaltenden Gravitationsgesetz sind nun mit einem Schlage diese Zweifel bestätigt. Dieses Gesetz ist der kosmische Prozeß, der den 2.Hauptsatz der Wärmelehre umkehrt und damit auf lange Sicht aufhebt, und zwar deshalb, weil die Eigenschaften „Energie“, „Masse“ und „Gravitation“ nicht trennbar sind. Sie sind Aspekte eines einzigen physikalischen Prinzips. Existiert nach Energie-erhaltender Gravitation eine dieser Größen, dann liegen auch die anderen fest und bestimmen das dynamische Verhalten aller physikalischen Prozesse dieses Systems. Zu jeder Energie existiert immer auch die ihr äquivalente Masse und deren Gravitation. Dabei ist es gleichgültig, in welcher Form die Energie vorliegt. Ein und derselbe Körper hat im heißen Zustand eine größere Masse und damit größere Gravitation als im kalten. Erwirbt nun dieser Körper in einem Gravitationsfeld kinetische Energie, dann anteilmäßig auch auf Kosten der Masse der in ihm gespeicherten Wärmeenergie, auch dann, wenn die Wärme das tiefste mögliche Temperaturniveau hat. Mit anderen Worten:

Auch der aus nicht nutzbarer Wärme bestehende Energieanteil verwandelt sich beim Fallen im Gravitationsfeld in vollständig nutzbare kinetische Energie! Das ist die Umkehrung des 2. Hauptsatzes der Wärmelehre, und das ändert unser kosmisches Weltbild grundlegend.

Mit einem mal ist es widerspruchslos möglich oder zumindest vorstellbar, die heutigen Beobachtungen versuchsweise wie folgt zu deuten:

In großen Sternsystemen, vor allen innerhalb von Galaxien, entstehen Sterne und Planeten durch gravitatives Zusammenballen von im Raum verteilter Materie. Dabei können günstige Bedingungen für die Entwicklung lebender Organismen entstehen. Während die Sterne ihren Energievorrat aufbrauchen
spiralen sie allmählich gegen ein galaktisches Zentrum. Weil ihr Drehimpuls außen bleibt, kollabieren schließlich alle ihre Massen infolge wachsender gegenseitiger Gravitation. Das „Ende“ ist ein mehr oder weniger explosiver Prozeß mit Materieauswurf und Zerstrahlung, wofür die axiale Richtung bevorzugt ist, weil diese Richtung nicht von kollabierender Materie oder von Magnetfeldern blockiert ist. Die ausgestoßene Materie verteilt sich im Raum und kann Rohstoff für neue Sterne sein. Also gilt:

Das galaktische Zentrum ist eine Recycling-Maschine für Sterne!

Das ist ein vorstellbarer Prozeß, aber es bleiben zumindest einige Fragen offen: Kann sich auch Strahlung in körperliche Masse zurückverwandeln? Nach welchen Mechanismen oder Prinzipien? Ist die Kosmische Hintergrundstrahlung (einschließlich Teilchenstrahlung) vielleicht der Rest aus dieser Vergangenheit? Es wird sich lohnen, darüber nachzudenken.

2 Die Voraussetzungen der Physik

Im einleitenden Text wurden stillschweigend klassische und relativistische Prinzipien ohne Erklärung vorausgesetzt, z.B. Energieerhaltung, die klassischen Axiome von Newton, auch die absolute Konstanz der Lichtgeschwindigkeit mit relativistischen Folgerungen. Dies geschah nicht unbedacht, vielmehr aus der Erkenntnis, daß sich abstrakte Vorreden leicht als Schlafmittel erweisen. Der Autor hält es für
besser, wenn der Leser sich zunächst selbst Fragen stellt, als ihm Antworten zu geben, bevor Objekte, auf die sich Fragen beziehen können, vorgestellt sind. Haben wir denn unser Bild von der physikalischen Welt wirklich in systematischer Reihenfolge erworben – oder nicht vielmehr oft rückblickend, indem wir uns selbst ermutigten, scheinbar Begriffenes und „Selbstverständliches“ für fragwürdig zu halten?

Die Frage, auf welchen bewußten oder unbewußten Voraussetzungen unsere physikalischen Vorstellungen beruhen, können wir nur klären, wenn wir überhaupt Vorstellungen haben, auch wenn diese falsch sein sollten. Speziell in Mathematik und moderner Physik ist Klarheit über die Voraussetzungen unabdingbar, gerade dann, wenn diese NICHT beweisbar sind. Es klingt paradox, aber exakt wurden diese Wissenschaften erst, als sie auf unbeweisbare (und vermutlich nicht widerlegbare) Grundannahmen zurückgeführt wurden, nämlich auf AXIOME, oft mit gleicher Bedeutung PRINZIPIEN genannt.

Wenn man wie ich mitten in der Diskussion über Themen der relativistischen Physik steht, wird offensichtlich, welche Verwirrung oft auch unter Physikern herrscht. Man wird etwa konfrontiert mit der
Kritik, daß Einstein doch unmöglich nachgeprüft haben konnte, ob die Lichtgeschwindigkeit wirklich in allen bewegten Systemen und im Gravitationsfeld konstant ist. Weil alles zu prüfen unmöglich ist, sei seine ganze Theorie nur ein Phantasiegebilde, unbewiesen, vage, vielleicht sogar widerlegt.

Wer so argumentiert zeigt ein fundamentales Mißverstehen der Physik, denn die Konstanz der Lichtgeschwindigkeit ist kein Meßergebnis, sondern ein Axiom. Im Prinzip hätte dieses Axiom auch aufgestellt werden können, bevor die Lichtgeschwindigkeit meßbar wurde. Alle Axiome (Prinzipien) der Physik haben das Kennzeichen gemeinsam, UNBEWEISBAR zu sein. Das heißt: Sie können also gerade das NICHT sein, was diese Kritiker fordern, eben weil sie nicht Meßergebnisse sondern ANNAHMEN sind. Etwa das Prinzip der Erhaltung von Energie. Niemand kann es beweisen. Das einzige, was dessen
Annahme rechtfertigt, ist die Tatsache, daß es keine Beobachtung gibt, in denen es nicht erfüllt ist. Wird ein Prinzip durch eine einzige Messung widerlegt, dann ist es überhaupt widerlegt und muß als ungültig akzeptiert werden.

Ein anderes Kennzeichen eines jeden Prinzips ist, daß es durch kein anderes aufgehoben oder eingeschränkt werden kann. Es gibt keine Rangordnung unter ihnen, keine „stärkeren“ oder „schwächeren“. Entweder ein Prinzip gilt, dann immer und überall (was nicht beweisbar ist), oder es ist keines.

Um die vorliegende Arbeit und im Besonderen ihren relativistischen Inhalt verstehen zu können, müssen wir uns Klarheit verschaffen über den fundamentalen Unterschied zwischen den Axiomen der
Klassischen Physik und den relativistischen Prinzipien, natürlich auch bezüglich der Konsequenzen.

Mit vorliegender Arbeit wurde nichts Neues beschrieben, ausgenommen nur die Konsequenz aus der Messung, daß der Zeitverlauf und damit die Masse bei Annäherung an ein Gravitationszentrum abnimmt, und zwar bis Null, wenn sie das Zentrum erreichen würde. Die Fall-Geschwindigkeit der Masse hätte Lichtgeschwindigkeit erst im Gravitationszentrum. Je größer die Ausgangsmasse, umso stärker nimmt diese Masse ab, eben immer bis Null. In keinem Abstand R > 0 erscheint ein Ereignishorizont mit v = c und zugehöriger Masse > 0. Kurzum: Es gibt kein Schwarzes Loch. In dem Maß, wie die Masse abnimmt, verwandelt sie sich in kinetische Energie, die beim Zusammenprall mit unvorstellbar hohen Temperaturen die vollständige Abstrahlung von Teilchen und Photonen erzwingt.

Ein unerklärter Bereich bleibt nur dort, wo die Längen- und Massendefinition der Physik nicht anwendbar ist. Definiert ist ein „Massenabstand“ durch die Lichtlaufzeit. Deshalb ist ein Abstand nie genauer angebbar als bis zur Wellenlänge der Photonen. Je kürzer die Wellenlänge der Photonen, umso mehr Masse „verbrauchen“ sie von den Massen, deren Abstand sie messen, bis nichts mehr da ist. Dieser Fall ist mehrfach experimentell aufgetreten. Z.B. glaubte man beim Tunneleffekt, man hätte Überlichtgeschwindigkeit gemessen. In diesem Bereich ist die Relativitätstheorie mit der Quantenphysik verknüpft.

2.1 Relativistische und Klassische Prinzipien

Was sind Physikalische Grundeinheiten?

Mit Einsteins Veröffentlichung der Speziellen Relativitätstheorie 1905 und wenig später der Allgemeinen Theorie der Gravitation begann ein in der Wissenschaftsgeschichte beispielloser Wandel im
Verständnis der Natur. Dieser Wandel geht nicht allein auf Einstein zurück, er kündigte sich schon Jahrzehnte vorher an, zunächst in grundlegenden Arbeiten bedeutender Mathematiker über mehrdimensionale Geometrien, dann, um die Wende zum 20. Jahrhundert, in physikalisch konkreten Theorie-ansätzen über Raum und Zeit in bis dahin kaum geahnten Vorstellungen z.B. bei H. A. Lorentz und
H. Poincaré. Vollzogen bis zur letzten Konsequenz wurde die Abkehr von bisherigen Vorstellungen schließlich von Albert Einstein, und zwar so radikal, daß er manchmal selbst zögerte, d.h. inkonsequent blieb im Versuch, den von ihm teils intuitiv, teils mathematisch geahnten Wegen zu folgen. Die von Kopernikus, Galilei, Newton und anderen begründete Argumentation war in ihrer inneren Logik so überzeugend, daß Einsteins radikaler Neubeginn auch heute noch bei manchen Physikern zu heftigen Abwehrreaktionen führt, vielleicht weil er sich noch konsequenter als seine Vorgänger an logische Strenge hielt. Für eingefahrene Denkgewohnheiten ist „noch konsequenter“ oft schwer vorstellbar.

Die erste grundlegend neue Erkenntnis war die, daß es unmöglich ist, ein physikalisches Objekt, z.B. einen Körper, „an sich“ zu erfahren, etwa durch Beobachtung. Wir beobachten nie „ein Ding an sich“, z.B. sehen wir unsere Mitmenschen nicht. Was wir wirklich sehen, ob Dinge, ob Wesen, sind nur
Bilder, die wir von ihnen haben. Da wir nicht in die erlebte Innerlichkeit eines andern Wesens eindringen können, sehen oder erfahren wir nichts über das andere Wesen "an sich", wir erschließen es nur in
Analogie zu unserem eigenen Erleben. Prinzipiell können wir aber aus Analogie nie mehr und nie etwas anderes erschließen als das, was wir aus eigenem Erleben kennen. Sind wir farbenblind geboren, dann wissen wir nichts über die Farben, die ein anderes Wesen sieht, denn das, was wir davon sehen oder vielleicht messen können, ist eine Wirkung, doch gewiß nicht dessen Erlebnis der Farbe.

Das gilt auch für die physische Welt. Ein Körper kann auf einen anderen Körper nur reagieren so weit und so wie er ihn „wahr“ nimmt, das ist als Wirkung. Der andere Körper existiert für ihn nur durch das „wahr“ Genommene, nicht durch etwas, was im andern „wirklich“ ist. Was die andere Existenz „in sich“ ist, ja wie weit sie überhaupt existiert, ist physikalisch unwesentlich, wesentlich ist, was sie „im Beobachter“ hervorruft. Für den Beobachter gibt es keine anderen „Wirk“-lichkeiten als seine Bilder von der physikalischen Umwelt, natürlich einschließlich dessen, was er mit Meßinstrumenten „wahr“ nimmt. Auch Instrumente zeigen nur Wirkungen an. Es gibt nichts Objektiveres als das Subjektive.

Genau das wurde nun erstmalig mit der Relativitätstheorie für die physische Welt konkret ausgesprochen und berücksichtigt. Man sagt nicht mehr, ein Objekt hat die und die Länge, oder die und die
Masse, sondern man sagt nur, welche Länge oder Masse ein bestimmter Beobachter von einem Objekt wahrnimmt. Dessen Wahrnehmung hängt z. B. davon ab, ob sich das beobachtete Objekt relativ zu ihm bewegt, eigentlich eine Selbstverständlichkeit. Aber sie hängt auch vom Gravitationsfeld ab, und dieses wiederum ist abhängig von der Relativgeschwindigkeit. Beobachten wir z.B. von einer Station auf der Erde ein Raumfahrzeug, so messen wir, daß das Raumfahrzeug der Krümmung einer Ellipse um die Erde folgt. Aus der Abweichung von der Geraden schließen wir, daß es von der Erde in bestimmter Weise angezogen wird, das heißt, wir messen die Bahnkrümmung und folgern daraus, daß am Ort des Fahrzeuges ein bestimmtes Gravitationsfeld herrscht. Doch die Astronauten sehen das anders. Sie schweben in ihrem Fahrzeug, sehen sich bewegt nur relativ zum Fahrzeug, das für sie ein sogenanntes „Inertialsystem“ ist. Relativ zu diesem existiert keine orbitale Eigenbewegung, v = 0, und die Gravitation ist Null. Hätten sie weder Fenster noch Erinnerung an den Start, dann wüßten sie nichts vom Erdfeld und nichts von ihrer Bewegung relativ zum Feld einer im (kleinen) Fahrzeug durch nichts wahrnehmbaren Erde. Schwerelosigkeit gibt es z.B. auch im Inneren eines Flugzeugs bei geeignetem Sturzflug.

Längen und Massen sind also keine absoluten Größen, sie können ein Objekt nicht charakterisieren, weil von Lage und Geschwindigkeit des Beobachters abhängig. Wenn aber diese Größen relativ sind, dann geraten wir in Schwierigkeiten, sie überhaupt zu definieren. Z. B. wurde die Masseneinheit, das Gramm, durch 1 cm³ Wasser bei 0° C definiert, und das cm durch das Urmeter in Paris. Sind diese Eichgrößen veränderlich, dann können wir damit nicht zuverlässig messen. Die Relativitätstheorie ist nur durchführbar, wenn wir überall absolute, unveränderliche Maßstäbe für Länge und Masse, aber auch für die Zeit haben. Damit ist klar, daß die gesamte bisherige physikalische Logik in sich zusammenbricht, wenn es nicht gelingt, die Eichgrößen so zu definieren, daß sie für alle Beobachter gleich sind.

Dieses Problem wurde erst erkannt, als einige physikalische Beobachtungen ein zunächst unbegreifliches Resultat zeigten, nämlich, daß für jeden Beobachter, egal, wie er sich bewegt oder wo er sich befindet, die Lichtgeschwindigkeit immer die selbe ist, auch unabhängig von Bewegung und Ort der Lichtquelle. Die radikalste Schlußfolgerung aus dieser Beobachtung zog Einstein, indem er sämtliche physikalischen Grundgrößen als „relativ“ erkannte und damit als unbrauchbar zur Festlegung von Grundeinheiten. Die Grundgrößen, die mehr oder weniger klar Jahrtausende hindurch die unbezweifelbare Grundlage aller Definitionen und jeder Beobachtung waren, ersetzte er durch neue Definitionen, indem er die Logik umdrehte. „Definieren“ heißt „Zurückführen auf Axiome“. Statt die Lichtgeschwindigkeit aus der Messung von Strecke und Zeit abzuleiten ging er umgekehrt vor: Er definierte Länge und Zeit, also Größen, die bislang von vornherein mit dem Körper als absolut gegeben erschienen, gegeben als „selbstverständliche“ und unveränderliche Eigenschaften der Körper. Nun aber definierte Einstein
Länge und Zeit durch das Licht! War das „an sich“ unabänderlich Gegebene für Newton Raum und Zeit, so erhob jetzt Einstein das Licht im Vakuum zum Axiom des absolut Gegebenen!

Weder Raum noch Zeit, sondern Licht sei die gesuchte vom Beobachter unabhängige Eichgröße, auf die alle Eichgrößen zu gründen sind. Ist das möglich? Es ist möglich, sogar besonders einfach. Dazu ist nichts weiter nötig als nur ein Lichtstrahl im Vakuum, ausgestrahlt vom ruhenden Atom eines bestimmten Elements. Jeder derartige Lichtstrahl bietet Eichmaße: Für die Einheit der Länge die Wellenlänge, für die Einheit der Zeit die Periodendauer. Um möglichst problemlos an bisher verwendete Einheiten anzuschließen fügt man zweckmäßig an jedes Eichmaß einen passenden konstanten Skalenfaktor.

(2.1)   Dann ist das Verhältnis   die absolut konstante Lichtgeschwindigkeit c.

Erzeugt l die Längeneinheit und t die Zeiteinheit, beides festgelegt durch Licht, dann herrscht die
Spezielle Relativitätstheorie. Natürlich wurde diese Theorie nur anerkannt, weil sie ausnahmslos von allen Beobachtungen und Experimenten als widerspruchsfrei bestätigt wurde. Wenn also behauptet wird, im Widerspruch zur Speziellen Relativitätstheorie sei eine höhere Geschwindigkeit als die des Lichts gemessen worden, dann wurde die Theorie nicht verstanden und fälschlich statt mit Licht mit Maßstäben der Klassischen Physik gemessen. Es gibt allerdings Messungen, nach denen eine
Geschwindigkeit größer zu sein schien als die des Lichts. Darauf gehe ich später ein. Zunächst aber geht es darum, herauszufinden, wie Einstein gedacht hat. Denn wie die meisten großen Entdecker hat auch er seine Theorie nicht aus genialen Postulaten geschöpft, vielmehr hat er auf diese Postulate erst hinterher geschlossen, ohne zu berichten, auf welchen Umwegen er dazu fand.

Zunächst wurde klar: Das Axiom der Konstanz der Lichtgeschwindigkeit macht nicht nur Länge und Zeit zu relativen Größen, sondern auch die Masse, bisher Inbegriff des Unwandelbaren. Alle Größen zeigen sich als abhängig von der relativen Geschwindigkeit des Objekts zum Beobachter, und, noch aufregender, Masse und Energie erwiesen sich als identisch, ein zu Newtons Zeit unvorstellbarer
Gedanke. Eine Uhrfeder wird also durch Aufziehen schwerer, wenn auch unmeßbar wenig. Aber an beschleunigten Elementarteilchen ist die Masse der Bewegungsenergie meßbar und übertrifft die Ausgangsmasse oft um ein Vielfaches. Die klassische Mechanik wird somit abgelöst durch eine neue Physik, die „Spezielle Relativitätstheorie“, die sich ausnahmslos in allen und ungezählten Beobachtungen und Anwendungen bestätigt.

Prinzipiell lassen sich unter der Voraussetzung der absoluten Konstanz der Lichtgeschwindigkeit die Grundeinheiten der Physik mit Licht einer bestimmten Spektralfreque n definieren, zunächst die

Zeiteinheit = t = 1 und die Längeneinheit = l = 1. Die Masseneinheit folgt daraus wegen E = m.c² und der Existenz von Lichtquanten E = hn, die dem Atom nur diskrete Spektralfrequenzen erlauben. Durch geeignete Skalenfaktoren läßt sich allein darauf, also auf Eigenschaften des Lichts, das
cm-gramm-sekunden (cgs)-System gründen).

2.2 Die Gleichungen der Speziellen Relativitätstheorie

Es ist unmöglich die Relativitätstheorie auch nur oberflächlich zu verstehen, wenn man sich nicht im Klaren darüber ist, daß die physikalischen Größen Länge, Zeit und Masse NICHT „Eigenschaften der physikalischen Objekte“ sind. Sie sind vielmehr Eigenschaften in der Vorstellung des jeweiligen
Beobachters. Die ganze Physik handelt also von den Gesetzmäßigkeiten zwischen diesen vorgestellten Begriffen, die ein Beobachter von diesen Objekten hat, wenn er sich unter bestimmten Bedingungen
(Relativgeschwindigkeit, Gravitationsfeld) zu einer bestimmten definierten Zeit an einem bestimmten definierten Ort aufhält oder aufhalten würde.

Ab sofort gilt also: Wenn wir sagen, ein Körper „hat“ die und die Masse oder Abmessung zu der und der Zeit, dann meinen wir nicht den Körper an sich, sondern das Bild des Körpers, das der Beobachter davon zu der vom ihm angegebenen Zeit hat. Über Eigenschaften des „Körpers an sich“ wissen wir nichts, es sei denn wir meinen unsere eigene Innerlichkeit als lebendiges Wesen.

Als „Beobachter“ gelten nicht nur lebendige Wesen. Alle physikalischen Objekte „beobachten“ alle anderen Objekte durch die Wirkungen, die sie in ihnen hervorrufen, und nur durch die Wirkungen, nicht durch das, was die Objekte  in sich  „wirklich“ sind.

Als bekannt vorausgesetzt werden hier die Gleichungen der Speziellen Relativitätstheorie bezüglich der Geschwindigkeitsabhängigkeit, die aus dem Postulat der absoluten Konstanz der Lichtgeschwindigkeit abgeleitet wurden. Ein Theorem allerdings wird man darunter vergeblich suchen, nämlich eine entsprechende Abhängigkeit vom Gravitationsfeld. Die Gleichungen gelten bei Abwesenheit von Gravitation.

Diese Gleichungen repräsentieren die sogenannte „Lorentz-Transformation“ und sind mit E = mc2 Basis und Voraussetzung für alle folgenden Ableitungen.

Dm = m – mo

            1. Massenzunahme von m_o um Dm auf m:      m = ;

            2. Zeitdilatation (Zeitintervalle verlängert):      T = ;

(2.2)   3. Additionstheorem für Geschwindigkeiten:   v = ;

            4. Längenkontraktion (Strecken schrumpfen):           L = L_o

            5. Dopplereffekt:                                           l = l_o.

„Lorentz-Invarianz“ ist die Bezeichnung dafür, daß diese Gleichungen überall im Universum unabhängig von Ort und Zeit gelten. Mit anderen Worten: Das Universum ist überall „sich selbst ähnlich“.

Aus der Äquivalenz von Masse und Energie E = mc² (bzw. m = E/c²) folgt, daß die Massenzunahme Dm = m–m_o gerade die Masse der kinetischen Energie sein muß:  Dm = E_kin/c². Sie entsteht ja dadurch, daß man der Masse m_o die Geschwindigkeit v erteilt. Einer Masse „m_o die Geschwindigkeit v erteilen“ bezeichnet also den Transport einer Masse (Energie) Dm = E_kin/c² von außen in die Masse m_o.

Die Massenzunahme mit v wird auf folgender Seite 15 bewiesen. Auf die Ableitung der anderen Gleichungen sei hier verzichtet, weil es dazu unübertroffen gute und leicht verständliche Darstellungen gibt.

Von allen empfehlenswerten Darstellungen seien aus Platzgründen nur zwei erwähnt:

1. Hermann Bondi: „Einsteins Einmaleins, Einführung in die Relativitätstheorie“. 120 Seiten (vergriffen?) TR-Verlagsunion in Verbindung mit Droemer Knaur München 1971. (Englisch: „Relativity and Common Sense – a new Approach to Einstein). Aus didaktischen Gründen arbeitet Bondy nicht mit dem relativistischen Wurzelausdruck, sondern mit dem sogenannten k-Faktor. Für Leser seines Buches gebe ich den Zusammenhang zwischen v und k an, wobei v für  v/c  steht, d.h. v wird im Verhältnis zur Lichtgeschwindigkeit c gemessen:

                        ,              ,         

2. Max Born: „Die Relativitätstheorie Einsteins“, 324 Seiten. ISBN 3-540-04540-6,     
Springer-Verlag Berlin Heidelberg NewYork Tokyo 1984

2.3 Relativistische Massenerhöhung durch Geschwindigkeit

Vorausgesetzt seien:

1. Die Äquivalenz von Masse und Energie, d. h. E = mc²,

2. Die absolute Konstanz der Lichtgeschwindigkeit c, und

3. Die Axiome von Newton, angewandt auf die nicht konstante Masse m = m(v).

Voraussetzung: Längs eines Weges  ds  wird Energie dE = Kds von außen zugeführt. Dafür gilt

[A]                  E = òK ds.                              (K = Kraft)

Nach Newton ist die Kraft definiert als die zeitliche Änderung des Impulses mv:

[B]                  K = d(mv)/dt = (dm/dt) v + m dv/dt.

[C]                  E = mc²           Diese drei Gleichungen findet man in Physikbüchern. Daraus folgt die

Behauptung: 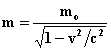                  worin  m_o = Ruhemasse (d.h. wenn v = 0)

[Für v² << c² gibt das die bekannte Näherungsgleichung    E = m₀ c² + m₀ v²/2].

Beweis:          Wir differenzieren Gleichung [A]:

[D]                  K = dE/ds = (dE/dt)/(ds/dt) = (dE/dt)/v.             Gleichgesetzt mit K aus [B] rechts:

(dE/dt)/v = (dm/dt) v + m dv/dt,          umgruppiert      dE/dt = (dm/dt) v² + m v dv/dt.

Wir erweitern die rechte Seite der letzten Gleichung mit c²/c² :

dE/dt = (dm/dt) c² v²/c² + (m c² v/c²) dv/dt. In die rechte Seite dieser Gleichung setzen wir ein

Gl. [C]    E = m c²   und deren Ableitung dE/dt = (dm/dt) c².   Wir erhalten:

dE/dt = (dE/dt) v²/c² + (E v/c²) dv/dt,     daraus

[E]                   (dE/dt) (1–v²/c²) = (E v/c²) dv/dt.

Wir schreiben abgekürzt:   A = (1–v²/c²) und die Ableitung   dA/dt = –(2 v/c²) dv/dt.  Damit wird [E]

                        (dE/dt) A = –(½) E dA/dt.        Multipliziert mit dt:        dE A = –(½) E dA,    oder

dE/E = –(½) dA/A.   Dies integriert mit den Grenzwerten: für v = 0  ist   E = E₀,  und  m = m_o:

(2.3)                E/E₀ = m/m₀ =    wie behauptet wurde.               m₀ = Ruhemasse

2.4 Definition der Masseneinheit durch Licht

Durch Einführung des Gravitationfeldes mittels der Poissonschen Gleichung konnte Einstein zwei Beobachtungen erklären, Periheldrehung der Bahnellipse von Planten und doppelte Lichtablenkung an der Sonne. Damit schien für Generationen von Physikern bewiesen, die Allgemeine Gravitation ergäbe sich aus Poissons Gleichung, ein folgenschwerer Irrtum. Periheldrehung und doppelte Lichtablenkung sind vielmehr das Werk eines blinden Passagiers, unbemerkt mit dieser Gleichung eingeschleppt, nämlich die absolute Konstanz der Lichtgeschwindigkeit. Läßt man nämlich die Poissonsche Gleichung (und die mit ihr definierte Quellenfreiheit des Feldes) weg, dann führt uns die Konstanz der Lichtgeschwindigkeit ganz allein und auf kürzerem Weg zu allen meßbaren relativistischen Resultaten.

Hätte Einstein das Relativitätsprinzip konsequent auch auf die Masse angewandt, dann hätte er natürlich erkannt, daß Gravitation ohne verzerrte Raumkrümmung möglich und ohne Tensoralgorithmus beschreibbar ist, weil nach Entfernung der Unendlichkeitsstellen die Raumkrümmung überall gering ist. Dazu ist nur notwendig, auch die dritte physikalische Grundgröße, die Masseneinheit, relativistisch zu definieren, das heißt durch das Licht, so wie er es für Länge (d. h. Raum) und Zeit getan hat.

2.5 Einsteins hypothetischer Raum

Einstein suchte eine Erklärung für das Rätsel der Gravitation. Dazu hatte er eine Idee. Ist Gravitation vielleicht eine Eigenschaft der Raumgeometrie?

Obwohl wir wenig wissen, welche Gedanken Einstein zur Prüfung dieser Vermutung verfolgt und wo er Sackgassen erkannt hat, können wir doch aus den Axiomen, die er nachträglich seinem Gedankengebäude vorangestellt hat, den Gang seines Denkens zuverlässig rekonstruieren.

„

In seinem Buch „Grundzüge der Relativitätstheorie“ geht Einstein von einem „Energietensor der
Materie“ aus, von dem er annimmt, daß dessen Divergenz verschwindet. Weil sich wahrscheinlich nicht alle Leser dieser Abhandlung darunter etwas vorstellen können, will ich diese Begriffe weder erklären noch verwenden, sondern mich auf den Hinweis beschränken, daß sie von Einstein aus der klassischen Physik entnommen wurden. Diesen Tensor, also einen klassischen Begriff, machte er zur Voraussetzung seiner Allgemeinen Theorie der Gravitation, die deshalb mit dieser Voraussetzung steht oder fällt.
Einstein spezifiziert diesen Tensor ohne weitere Rechtfertigung mit folgenden Worten:

1.      Er soll keine höheren als zweite Differentialquotienten der g_mn enthalten.

2.      Er soll in diesen zweiten Differentialquotienten linear sein.

3.      Seine Divergenz soll identisch verschwinden.“

Ich setze nicht voraus, daß jemand diese Axiome versteht. Der Leser möge nicht ungehalten sein, wenn ich erst nachfolgend klar mache, warum ich sie überhaupt zitiere. Bei jedem dieser Axiome müßte man fragen: Warum? Einstein rechtfertigt keines dieser Axiome, auch nicht, nachdem er ergänzt:

„Die ersten beiden dieser Bedingungen sind natürlich der POISSONSCHEN Gleichung entnommen.“

Hier versuche ich also nicht, den Tensoralgorithmus zu diesen Axiomen darzustellen oder gar zu erklären, sondern ich will nur auf Folgendes hinweisen, was in allen Lehrbüchern nachgelesen werden kann.

Darin steht zunächst die bekannte klassische Grundgleichung für Gravitation, nämlich

(2.4)        Gravitationskraft .         (G = Gravitationskonstante, R = Abstand der Massen.

Wie in Lehrbüchern mathematisch bewiesen, gilt diese Gleichung exakt für kugelsymmetrische Massen M und m, die sich verhalten, also ob jede Masse in ihrem Mittelpunkt konzentriert wäre. Ist nicht jede kugelsymmetrisch über den Raum verteilt, dann muß man sich die Massen nach einer Dichteverteilung aus punktförmigen Massenelementen dM und dm zusammengesetzt denken. Durch Integration kann man dann mit Gl.(2.4) die Kraft berechnen, die auf jedes Gebilde aus Massenelementen wirkt (für Gravitation wird das Gesetz linearer Überlagerung vorausgesetzt). Auch in diesem Fall gilt also das klassische Gesetz von Newton, nur ist es dann als Differentialgleichung zu formulieren. Dies tat der Mathematiker S. D. Poisson. Mit der auf die Poissonsche Gleichung gegründeten Potentialtheorie übernahm Einstein eine nicht-relativistische Voraussetzung. Das betont er durch die oben angegebenen drei Axiome.
Obwohl von den größten Mathematikern entwickelt gilt aber die Potentialtheorie nicht für Massen, die relativistisch veränderlich sind, denn daß Massen sich durch Energieaustausch verändern könnten war diesen Mathematikern noch ganz unvorstellbar. Mit der Poissonschen anstelle der Newtonschen Gleichung erhielt Einstein zwar eine allgemeinere Formulierung, aber klassisch ist sie immer noch, und
damit ist auch die axiomatische Voraussetzung seiner gesamten Theorie klassisch.

Die drei genannten Axiome ergänzte Einstein durch das Axiom der Konstanz der Lichtgeschwindigkeit, das er mittels des Intervalls einführt. Dann leitet er aus diesen Axiomen die Maßstäbe ab, die für Länge und Zeit im Gravitationsfeld gelten. Er kombiniert also die Konstanz der Lichtgeschwindigkeit mit der klassischen Poissonschen Gleichung. Weil diese aus dem Newtonschen Gravitationsgesetz
abgeleitet ist, gilt alles nur unter der Voraussetzung dieses Gesetzes, nämlich daß die Fall-Energie im quellenfreien  „Feld“ entsteht. Das heißt, auch bei Einstein „entsteht“ diese Energie  ohne Quelle, was er ausdrücklich hervorhebt. Nirgends hat er je die Massen als mögliche Energiequelle genannt.

Ohne auf Einsteins Rechnung einzugehen sei die Formel für den Zeitmaßstab, den er aus dieser
klassischen Voraussetzung und der Konstanz der Lichtgeschwindigkeit abgeleitet hat, hier zitiert:

(A)   .   Für 2GM/c²R<<1  ist (B)   t @ t_o(1– GM/c²R)  oder  t_o @ t(1+ GM/c²R)

(Zeitintervalle:  t gilt in unendlicher Entfernung, t_o gilt nach Annäherung bis zum Abstand R.)

Dann folgert Einstein korrekt: „Die Ganggeschwindigkeit einer Uhr ist also desto geringer, je mehr
ponderable Massen in ihrer Nähe sind“. (Den Beobachter denke man sich außerhalb der Massen.)

Da Einstein diese Formel in anderer Schreibweise darstellt, zitiere ich sie im Anhang (Seite 87) in seiner Formulierung mit der Übersetzung in die übliche, von mir bevorzugte physikalische Schreibweise.

Vielleicht wird mir der Leser dankbar sein, wenn ich nach dieser vereinfachten Einsteinschen Darstellung zeige, wie man dieselbe Formel (A) direkt aus den klassischen Formeln erhält. An dieser Formel läßt sich dann der Widerspruch zu Energie-Erhaltung und zum Relativitätsprinzip aufzeigen.

Nach dem Klassischen Gesetz gilt für die durch freien Fall einer Masse m von Unendlich bis R entstehende Geschwindigkeit . Daraus die kinetische Energie E_kin= mv²/2 = GMm/R. Ausdrücklich wird stets betont, daß diese Energie im Feld „entsteht“. Die innere Energie von m  ist mc², also ist  E_kin/mc² = GM/c²R. Das ist gerade der Anteil, um den das Zeitintervall in der Näherungsformel (B) im Abstand R größer ist als bei R= ¥ (die Näherung ist für v<<c zulässig). Weil nach Poisson die Energie aus dem Feld und nicht aus der fallenden Masse bezogen wird, nimmt die Masse im Fallen nicht ab.

In der klassischen Theorie ist ein möglicher Anfangsbetrag der Potentiellen Energie prinzipiell
unbekannt. Bekannt ist nur deren Änderung. Beim Freien Fall aus Unendlich ist diese Änderung
E_pot = –GMm/R, also gleich der entstehenden kinetischen Energie. Setzt man aber voraus, daß mc² die anfängliche potentielle Energie ist, dann nimmt diese also ab auf mc²–GMm/R und es verbleibt unten die Energie  mc² –. Wie zuvor ist  das Verhältnis dieser Änderung zu mc², das stimmt überein mit der Änderung in der Einsteinschen Formel (B). Mit dem Zeitintervall ändert sich also der Gang der Zeit mit dem gleichen Faktor wie die potentielle Energie, wenn man die Änderung auf die Energieeinheit der fallenden Masse bezieht, d. h. im Verhältnis zu mc². Die von Einstein aus der Poissonschen Voraussetzung abgeleitete Formel (B) erhielten wir jetzt direkt und, wohlgemerkt, ohne Tensoralgorithmus. Dazu haben wir (wie Einstein) für potentielle und kinetische Energie die klassischen Formeln vorausgesetzt. Ohne die klassischen Formeln hätte auch Einstein weder die Formel (A) noch deren Näherung (B) erhalten. Allerdings beweist die direkte Ableitung aus der Klassischen Physik, daß als Quelle für die Fall-Energie die innere Energie mc² der fallenden Masse vorauszusetzen ist, im Widerspruch zur Poissonschen Voraussetzung, die ja gerade das ausschließt.

Von da ab wird Einstein inkonsequent, weil er so weiterrechnet, als ob die von ihm voraussetzten Axiome relativistisch wären. Bei relativistischer Rechnung aber hätte er im Gravitationsgesetz Gl.(2.4) die Massen nicht als konstant annehmen dürfen, gleichgültig, ob in der Formulierung von Newton oder von Poisson. Außerdem gilt in der Speziellen Relativitätstheorie der Erhaltungssatz für Energie, während in der Klassischen Theorie die Fall-Energie „entsteht“, und zwar aus dem leeren Raum. Wenn man glaubt, Energieerhaltung wäre gerettet, indem man den leeren Raum einfach „Feld“ nennt und dazu sagt: „Die
Summe aus Potentieller und Kinetischer Energie ist konstant.“, dann zaubert man mit einem Taschenspielertrick. Denn Konstanz an sich macht aus dem quellenfreien Feld noch lange keine Energiequelle.

Einstein war sich dessen natürlich bewußt. Er „löste“ aber das Problem, indem er mit folgendem kaum merklichen Nebensatz ein durch keine Erfahrung begründbares Axiom anfügt ohne es als Axiom zu kennzeichnen: „Es ist zu bedenken, daß es außer der Energiedichte der Materie auch eine Energiedichte des Gravitationsfeldes geben muß, so daß von einem Erhaltungssatz für die Energie (bzw. des Impulses) der Materie allein nicht die Rede sein kann.“ (Kursiv hervorgehoben durch Einstein). Hier entspringt das Problem, das er nicht lösen konnte, als er die Möglichkeit Schwarzer Löcher zu widerlegen suchte. Er wußte natürlich, daß die Singularität Schwarzer Löcher auch dann nicht verschwindet, wenn er
unendlich dichte Punktmassen ausschließt (eben durch Poissons räumliche Massenverteilung). Hätte er relativistische Voraussetzungen gemacht, dann hätte er anstelle des Klammerausdrucks in Gl.(A) und (B) den Faktor e^–a/R der Energie-erhaltenden Gravitation erhalten, wie auf den Seiten 5-6 erklärt.

Einstein gibt nirgends an, mit welcher Messung sich seine hypothetische „Energiedichte des Gravita-tionsfeldes“ nachweisen ließe. Mit dieser Hypothese gerät seine Theorie in Widerspruch zu sich selbst. Einerseits nimmt in obigen Gleichungen die fallende Masse nicht ab (weil sein Feld und nicht die Masse die Energie des freien Falles liefert). Andererseits führten die selben Formeln zu seiner empirisch bestätigten Voraussage, daß die Zeit umso langsamer abläuft je größer das Gravitationsfeld ist („je mehr ponderable Masse in ihrer Nähe sind“). Dann schwingen die Atome, also die Taktgeber der Uhr, langsamer. Die atomaren Schwingungen sind aber proportional der atomaren Masse, folglich muß, im
Widerspruch zur Voraussetzung, die Masse bei Annäherung an andere Massen eben doch abnehmen.

Dieser Widerspruch ist nicht lösbar. Weil bei Einstein die fallende Masse nicht abnimmt behält sie ihre Gravitationswirkung, müßte sogar zunehmen, wenn man auch der entstehenden kinetischen Energie Gravitation zuschreibt. Die Folge ist, daß die Fallgeschwindigkeit beim sogenannten Schwarzschild-Radius Lichtgeschwindigkeit erreicht (was übrigens unendlicher Energie entspricht!).

Das wäre ein Schwarzes Loch. Es ließe sich nur vermeiden durch Ausnahme-Axiome. Jedenfalls aber erfordern die Widersprüche Zusatzaxiome. Es dürfte ein aussichtsloses Unterfangen sein, alle im komplizierten mathematischen Algorithmus verborgenen Widersprüche aufzudecken und zu beseitigen.

Um Mißverständnissen im Voraus entgegenzuwirken möchte ich an dieser Stelle hervorheben, daß die Klärung dieser Widersprüche Einstein selbst zu verdanken ist. Die Widersprüche heben also die
Bedeutung seines Lebenswerkes keineswegs auf. Er kam zu seinen Erkenntnissen wohl kaum auf dem Weg, dem ich hier anhand seiner eigenen axiomatischen Darstellung folgte. Es scheint mir wenig wahrscheinlich, daß er von den genannten Axiomen ausging. Sein Motiv war ja die geniale Intuition, daß die Gravitation eine Erscheinung der Raumgeometrie sein könnte. Daraus ist zu schließen, daß er an das Problem gar nicht physikalisch heranging, vielmehr aus der Idee, die Gravitation als Eigenschaft der vierdimensionalen gekrümmten Raumgeometrie nachzuweisen, eine Idee, die ihn seit seiner Studienzeit faszinierte und ein Leben lang inspirierte. Weil ihm das für viele Erscheinungen überzeugend gelang, gewann er die Zuversicht, die paar verbliebenen Widersprüche mit Schwarzen Löchern und Energie-Erhaltung würden sich früher oder später lösen. Die oben genannten Axiome paßten zu gut zu seinem geometrischen Modell und stützten seine Gewißheit, auf der richtigen Spur zu sein. Die Freiheit seines Denkens erlaubte ihm, mit der Idee einer „Weltformel“ zu spielen, aber sie führte eben auch dazu, das Relativitätsprinzip in voller Tragweite zu erkennen, wofür allein sich diese Denkweise gelohnt hätte.

Aber alle Hypothesen, die von vielen kompetenten Mathematikern zur relativistischen Gravitation versucht worden sind, führten hartnäckig immer wieder auf das gleiche Problem, nämlich daß sich in der Umgebung Schwarzer Löcher unerforschbare weiße Flecken ergaben. Doch statt an der Theorie zu zweifeln, zog man vor, sich zu beruhigen. Verglichen mit allen denkbaren Theorien hatte das Gravitationsgesetz von Newton einen offensichtlichen Vorzug, nämlich dem physikalischen Ideal, die Natur so einfach wie möglich zu beschreiben, am nächsten zu sein. Wenn wegen der Unendlichkeitsstellen sogar das einfachste Gesetz so kompliziert ist, dann konnte man die „unlösbaren Probleme“ einfach als Indiz ansehen, daß dort alles noch komplizierter sein mußte, aber „irgendwann“ eben doch lösbar.

Für seine Allgemeine Theorie der Gravitation konnte Einstein auf die für gekrümmte Räume hochentwickelte Potentialtheorie zurückgreifen. In dieser Theorie gab es kaum eine Frage, die nicht von den bedeutendsten Mathematikern gründlich untersucht und aufgeklärt worden wäre. Was Einstein bezüglich mehrdimensionaler gekrümmter Räume vorfand, war, wie es schien, ein riesiger Vorrat jeder nur denkbaren Möglichkeit. Doch die Potentialtheorie wurde von Denkern geprägt, die mehr Mathematiker als Physiker waren. Ihre Hauptsätze entstanden zudem in einer Zeit, da einige der wichtigsten Grundprinzipien der Physik noch gar nicht oder nicht in ihrer Allgemeinheit erkannt waren. Dazu gehört Erhaltung von Energie. Man konnte also in der Illusion leben, alle nur denkbaren Zentralkräfte und die zugehörige Theorie zu kennen. Solange aber Energieerhaltung noch nicht zu Ende gedacht war, konnte auch das größte Genie Energieerhaltung nicht in die Potentialtheorie einbeziehen. Zwar wurde früh erkannt, daß im Newtonschen Gesetz die Summe aus potentieller und kinetischer Energie konstant ist, aber vor
Einstein lag es außerhalb des Denkbaren, daß die Masse selbst Energie sein könnte.

Hätte sich Einstein dem Bann der Mathematiker entzogen und mit seinem Prinzip E = mc² das Gravitationsgesetz an Energieerhaltung adaptiert, dann wäre ihm nicht entgangen, daß das Gesetz von Newton (auch in Poissons Fassung) eben nicht das einfachst mögliche Gesetz ist. Was jede bis heute versuchte Raumgeometrie unlösbar kompliziert ist deren Singularität. „Singularität“ nennt man die Stelle, wo die Gravitationskraft und damit die Energie unendlich wird, weil dort die fallende Masse Lichtgeschwindigkeit erreicht. Bezieht man aber Energieerhaltung in das Newtonsche Gesetz ein, dann geschieht, was niemand erwartet hatte: Die Singularität verschwindet, mit dieser die Notwendigkeit, alle anderen physikalischen Prinzipien so zu „verbiegen“, daß sie sich, wie man fälschlich hoffte, widerspruchsfrei in die zusätzliche Raumkrümmung einzwängen lassen. Gerade wegen der inneren Widersprüche ist eine solche Anpassung logisch unmöglich.

Auf die Idee, mittels relativistischer Massen Energie-Erhaltung einzubeziehen, konnte also Einstein eben aus dem Grund nicht kommen, weil er die Gravitation durch Raumkrümmung erklären wollte. Dazu benötigte er genau die Verzerrung der Raumkrümmung, auf der diese Singularität beruht.